문제 설명
신비로운 유적 탐험
카카오 고고학 연구팀은 20,000년 전 문명의 발상지를 조사하던 중 벽면에 그려진 비슷한 모양의 그림을 여러 개 발견하게 되었다. 각각의 그림은 트리 형태로 구성되어 있으며 그림의 일부가 유실되어 전체의 정보를 해독할 수는 없었다.
연구팀은 이 그림들이 특정한 부족의 가계도를 그린 것으로 추정하였다. 트리의 루트는 부족의 조상을 의미하며, 루트의 자식들은 트리 상에서 부모-자식 관계로 연결되어 있고, 그들의 자식은 또 새로운 가지로 연결되어 있는 식이다. 이렇게 가족 전체의 관계가 여러 개의 (같은 모양의) 그림으로 남아있으며, 유실된 정보를 제외하고 공통적으로 남아있는 정보를 토대로 이 부족에 대한 연구를 진행할 수 있다고 판단하였다. 다행히 그림의 중심부에는 유실의 흔적이 없어 두 그림의 루트는 같은 사람을 의미한다고 간주할 수 있었다.
아래 그림은 서로 다른 두 그림에서 얻은 정보를 보기 좋은 형태로 나타낸 것이다. 트리의 번호들은 한 트리에서 각각의 정점을 구별하기 위한 것으로 두 트리의 같은 번호가 같은 사람이라는 의미는 아니다.
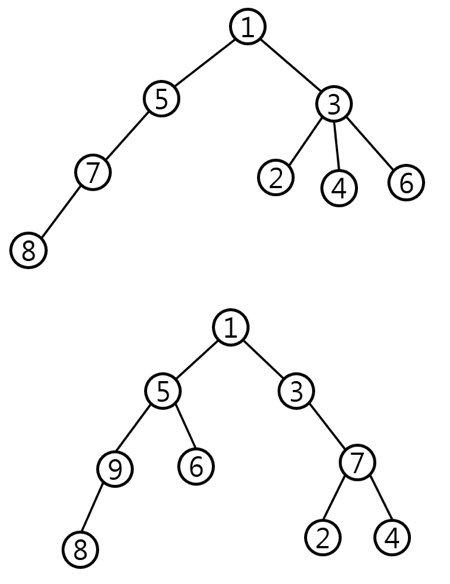
가설이 맞는지를 확인하기 위해, 두 그림에서 얻은 트리의 공통부분이 얼마나 되는지를 알아보고 싶다. 그림에서 확인할 수 있는 정보는 상대적인 부모-자식 관계가 전부이기 때문에 자식들의 이름이나 순서 등의 정보는 없다. 따라서 자식들의 순서를 무시하고, 각 트리의 루트를 포함하는 부분 트리로서 두 트리에 모두 포함되는 트리를 공통부분으로 정의하자.
두 개의 트리를 입력으로 받아 최대 공통부분의 크기를 계산하는 프로그램을 작성하라.
입력 형식
입력은 두 트리를 나타내는 n1, g1, n2, g2로 주어진다. n1, n2는 각 트리의 노드 수를 의미한다. g1, g2는 트리의 정보를 나타내는 값으로, 각각 크기가 (n1 - 1) × 2와 (n2 - 1) × 2인 2차원 배열로 주어진다. g1, g2의 각각의 행은 연결된 두 노드를 의미하는데, 두 개의 값 중 하나가 부모 노드의 번호, 다른 하나가 자식 노드의 번호이다. 입력되는 값의 제한조건은 아래와 같다.
1 <= n1, n2 <= 100- 노드 번호는 각각
1부터n1,n2까지의 값이 사용되며, 각 트리의1번 노드가 루트이다. - 입력되는 데이터는 항상 올바른 트리임이 보장된다.
출력 형식
두 트리의 최대 공통부분의 노드 수를 리턴한다.
예제 입출력
| param | value |
|---|---|
| n1 | 8 |
| g1 | [[3, 1], [5, 7], [8, 7], [2, 3], [3, 6], [1, 5], [4, 3]] |
| n2 | 9 |
| g2 | [[1, 5], [5, 6], [3, 7], [3, 1], [7, 4], [7, 2], [9, 8], [5, 9]] |
| answer | 7 |
예제에 대한 설명
본문의 그림과 같은 예이다. 첫 번째 트리에서 1, 2, 3, 4, 5, 7, 8번의 사용자를 포함하는 트리는 두 번째 트리에서 1, 3, 4, 5, 6, 7, 9번 사용자를 포함하는 트리와 모양이 동일하며, 이것이 가장 큰 경우이다.